Teorema de Pitágoras: Altura e Área do Triângulo Equilátero
O Teorema de Pitágoras possui grande importância na construção de fórmulas, uma dessas generalizações acontece no estabelecimento de uma fórmula geral para calcular a altura e a área de um triângulo equilátero, esse tipo de triângulo possui os lados e os ângulos internos com medidas iguais.
Observe as demonstrações a seguir:
Altura do triângulo equilátero
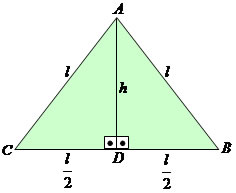
Dado o triângulo ABC, vamos estabelecer uma expressão geral para o cálculo da altura.
Observe que a altura (h) do triângulo ABC, corresponde ao cateto do triângulo ADB, então podemos aplicar o Teorema de Pitágoras para calcular a altura (h) do triângulo ABC.
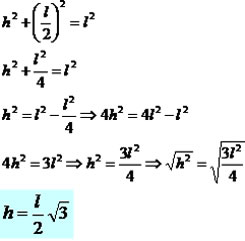
Área do triângulo equilátero
A área de um triângulo é definida pela metade do produto da área da base pela altura. Continuando a análise do triângulo ABC, vamos determinar uma expressão capaz de calcular a área de qualquer triângulo equilátero.
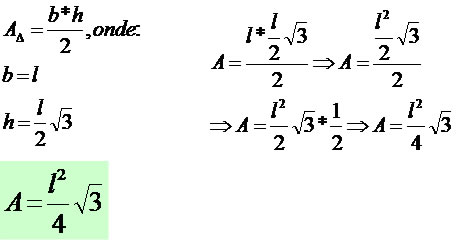
Podemos notar que as expressões estão todas em função da medida do lado do triângulo equilátero.
Exemplo 1
Determine a altura de um triângulo equilátero que possui perímetro igual a 30 cm.
Resolução:
Perímetro é a soma dos lados, então cada lado mede 10 cm.
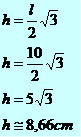
Exemplo 2
Calcule a área de uma figura que possui o formato de um triângulo equilátero com lados medindo 6 m.
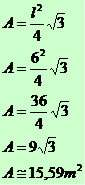
Exemplo 3
Calcule a área da região em negrito sabendo que o raio da circunferência vale 10 m e o lado do triângulo equilátero inscrito mede 7 m. Considere √3 = 1,7 e ∏ = 3,14.
Área do triângulo Área da circunferência
Área em negrito
314 – 20,83 = 293,17m2
Teorema de Ptolomeu
Sabemos de grandes matemáticos do passado e de suas variadas contribuições para os campos da álgebra, trigonometria, geometria e demais áreas da matemática, como Pitágoras, Arquimedes, Pascal, Heron de Alexandria e outros. Claudius Ptolomeu também foi um desses grandes matemáticos, além de astrônomo e geógrafo. Ptolomeu nasceu por volta do ano de 85 no Egito e morreu, aproximadamente, no ano de 165 em Alexandria, também no Egito. Foi Ptolomeu quem propôs a teoria do geocentrismo, que perdurou por cerca de 1400 anos.
Além de suas contribuições na astronomia e na geografia, Ptolomeu influenciou a matemática (em particular, a trigonometria) propondo um teorema que leva seu nome: Teorema de Ptolomeu. Vejamos o que diz esse teorema.
Considere um quadrilátero ABCD inscrito em uma circunferência, como mostra a figura. O teorema de Ptolomeu diz que: o produto das diagonais AC e BD é igual à soma dos produtos dos lados opostos.
Ou seja:
AC∙BD = AB∙CD + AD∙BC
Esse teorema é muito útil no estudo da trigonometria, pois, através dele, podemos obter o teorema de Pitágoras e, se combinado com a Lei dos Senos, conseguimos demonstrar as fórmulas de sen (a + b) e sen (a – b).
Vejamos um exemplo de aplicação do teorema de Ptolomeu.
Exemplo: Considere o quadrilátero ABCD inscrito numa circunferência, como mostra a figura.
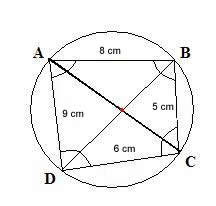
Sabendo que a diagonal AC mede 12 cm, determine a medida da diagonal BD.
Solução: Pelo teorema de Ptolomeu, temos que:
AC∙BD = AB∙CD + AD∙BC
Segue que:
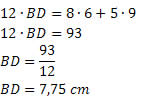
Teorema de Tales
O Teorema de Tales é determinado pela intersecção entre retas paralelas e transversais, que formam segmentos proporcionais. Foi estabelecido por Tales de Mileto que defendia a tese de que os raios solares que chegavam à Terra estavam na posição inclinados. Partindo desse principio básico observado na natureza, intitulou uma situação de proporcionalidade que relaciona as retas paralelas e as transversais.
Retas paralelas cortadas por retas transversais formam segmentos proporcionais. Observe:
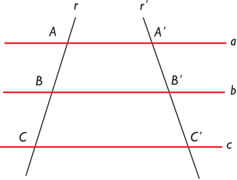
No esquema acima, as retas a, b e c são paralelas e as retas r e r’ são transversais, de acordo com o Teorema de Tales temos as seguintes proporcionalidades:
Observe que a relação estabelecida envolve noções de razão e proporção, o segmento AB está para o segmento BC assim como o segmento A’B’ está para o segmento B’C’. A igualdade entre as duas razões formam uma proporção, o cálculo dessa proporção será resolvido através de uma simples multiplicação cruzada, ou de acordo com a propriedade das proporções: o produto dos meios é igual ao produto dos extremos.
Observe o seguinte exemplo, nele aplicaremos o Teorema de Tales para encontrar o valor do segmento desconhecido:
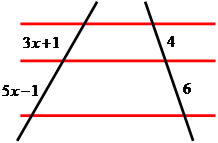
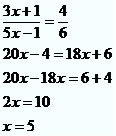
O Teorema de Tales possui inúmeras aplicações nas diversas situações envolvendo cálculo de distâncias inacessíveis, possui grande aplicabilidade nas questões relacionadas à Astronomia.
Tetraedro regular
O tetraedro regular é uma pirâmide regular que apresenta as quatro faces congruentes e as seis arestas também congruentes.
Cálculo da área total do tetraedro.
Como o tetraedro regular é composto por 4 faces triangulares e os triângulos das faces são equiláteros, a área total será dada por:
Onde,
a → é a medida da aresta do tetraedro.
A altura do tetraedro é um elemento que merece destaque. A fórmula para determinação da altura do tetraedro é:
Cálculo do volume do tetraedro
O volume do tetraedro, assim como o de qualquer pirâmide, é obtido fazendo:
Onde,
SB → é a área da base do tetraedro.
Como,
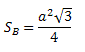
e
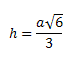
Obtemos:
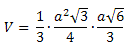
Ou
Exemplo: Calcule a área total e o volume de um tetraedro regular de 4 cm de aresta.
Solução: primeiro vamos calcular a área total.
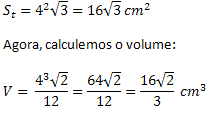
Unidades de Medida ao Longo da História
Ao longo da história da humanidade as unidades de medida eram criadas e adaptadas de acordo com a necessidade dos povos. Muitas dessas medidas eram realizadas baseadas em partes do corpo. Por exemplo, o cúbito era uma unidade utilizada pelos egípcios há, aproximadamente, 4.000 anos. Ela consistia na distância do cotovelo até a ponta do dedo médio do faraó.
O palmo também era muito utilizado pelos povos egípcios, essa medida consistia na utilização de quatro dedos juntos e correspondia à sétima parte do cúbito. Hoje o palmo ainda é utilizado em medições caseiras, é medido pela distância em linha reta do polegar ao dedo minguinho.
Algumas unidades ainda são utilizadas por determinados países até os dias atuais. A Inglaterra e os Estados Unidos utilizam a jarda como medida de comprimento. Essa medida consiste na distância entre o nariz e a ponta do polegar, com o braço esticado. Nos jogos de futebol, a jarda é utilizada nos momentos em que o juiz precisa marcar a distância entre a bola e a barreira, para isso ele faz a medição contando passos, que é a medida aproximada de 1 jarda. No futebol americano as distâncias percorridas pelos atletas são registradas em jardas, que medem aproximadamente 0,91 metros.
Unidades de Medida de Volume
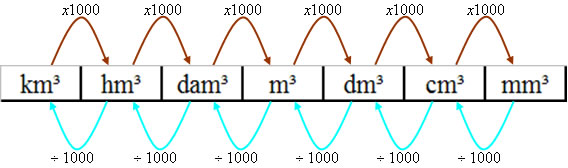
Definimos volume como o espaço ocupado por um corpo ou a capacidade que ele tem de comportar alguma substância. As figuras espaciais como o cubo, paralelepípedo, cone, pirâmide, cilindro, prismas, entre outras, possuem volume. A capacidade de um corpo é calculada através da multiplicação entre a área da base e a sua altura. A unidade usual de volume é utilizada de acordo com as unidades das dimensões do corpo. Observe as unidades de volume de acordo com o SI (Sistema Internacional de Medidas):
km³ = quilômetros cúbicos (km * km * km)
hm³ = hectômetros cúbicos (hm * hm * hm)
dam = decâmetros cúbicos (dam * dam * dam)
m³ = metros cúbicos (m * m * m)
dm³ = decímetro cúbico (dm * dm * dm)
cm³ = centímetro cúbico (cm * cm * cm)
mm³ = milímetro cúbico (mm * mm * mm)
Observe a tabela de transformações das unidades de medidas do volume.
1m³ (lê-se um metro cúbico) = 1000 litros
1dm³ (lê-se um decímetro cúbico) = 1 litro
1cm³ (lê-se um centímetro cúbico) = 1 mililitro (ml)
Exemplo 1
Calcule a capacidade, em litros, de uma piscina com as seguintes dimensões: 8 m de comprimento, 6 m de largura e 1,8 m de profundidade (altura).
Resolução:
Calculando o volume da piscina.
V = 8 * 6 * 1,8
V = 86,4 m³
Como 1m³ corresponde a 1000 litros, e a piscina possui 86,4m³ temos:
86,4 * 1000 = 86 400
Portanto, precisamos de 86 400 litros de água para encher uma piscina com as seguintes dimensões: 8m de comprimento x 6m de largura x 1,8m de profundidade.
Exemplo 2
Um reservatório possui volume de 3000m³. Qual a capacidade desse reservatório em litros?
Resolução:
Como 1m³ equivale a 1000 litros, temos que:
3000 * 1000 = 3 000 000
O reservatório possui capacidade igual a 3 000 000 de litros de água.
Unidades de Medidas de Área
O cálculo de áreas é uma parte da Geometria que possui uma variedade de aplicações no cotidiano. A área pode ser calculada através do produto entre duas dimensões do plano: comprimento x largura ou base x altura. Existem algumas expressões algébricas matemáticas que são associadas a figuras geométricas, possibilitando o cálculo de suas áreas. As unidades usuais de áreas, de acordo com o SI (sistema internacional de unidades), são a seguintes:
km² = quilômetro quadrado
hm² = hectômetro quadrado
dam² = decâmetro quadrado
m² = metro quadrado
dm² = decímetro quadrado
cm² = centímetro quadrado
mm² = milímetro quadrado
O procedimento para o cálculo da área de uma região plana exige que todas as dimensões estejam numa mesma unidade de comprimento, que de acordo com o SI são:
km = quilômetro
hm = hectômetro
dam = decâmetro
m = metro
dm = decímetro
cm = centímetro
mm = milímetro
As unidades de comprimento e de área podem ser transformadas de acordo com as seguintes tabelas de conversões de medidas:
Medidas de comprimento
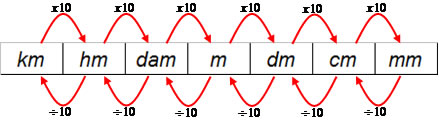
Transformando 1 metro (m) em milímetros (mm):
1º passo: transformar metro em decímetro
2º passo: transformar decímetro em centímetro
3º passo: transformar centímetro em milímetro
Para ser mais prático, podemos multiplicar o metro por 10x10x10 (1000)
1 x 10 x 10 x 10 = 1000 →1m = 1000mm
Medidas de Área
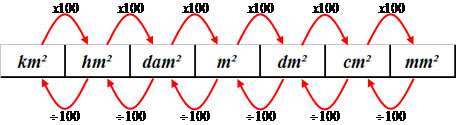
Transformando 1m² (metro quadrado) em cm² (centímetro quadrado)
1º passo: transformar m² em dm²
2º passo: transformar dm² em cm²
Pelo processo prático podemos multiplicar o m² por 100x100 (10 000)
1 x 100 x 100 = 10 000 → 1m² = 10 000cm²
Exemplo 1
Um muro com as seguintes medidas: 20m de comprimento e 2m de altura foi construído com tijolos de dimensões 20cm de comprimento e 20cm de altura. Quantos tijolos foram gastos na construção desse muro, descartando a hipótese de desperdício?
Área do muro
20m x 2m = 40m²
Área do tijolo
20cm x 20cm = 400cm²
A área do muro e a do tijolo estão em unidades diferentes, para isso devemos utilizar a tabela de conversões no intuito de igualar as medidas. Podemos escolher entre as seguintes transformações:
m² em cm² ou cm² em m²
Vamos transformar m² em cm²:
40 x 100 x 100 = 400 000 cm²
Para descobrir quantos tijolos foram gastos, basta dividirmos a área do muro em cm² pela área de um tijolo:
400 000 cm² : 400 cm² = 1000
Foram gastos 1000 tijolos na construção do muro.
Exemplo 2
Pedro deseja colocar cerâmica na área de lazer de sua casa, que possui 9 m de comprimento por 6 m de largura. Se forem usadas cerâmicas quadradas com lado medindo 100cm, quantas serão gastas?
Área em m²
9m x 6m = 54m²
Área da cerâmica em m²
100cm x 100cm = 10 000 cm²
Transformando cm² em m², temos:
10 000 : 100 : 100 = 1m²
54m² : 1m² = 54
Serão utilizadas 54 cerâmicas na área de lazer da casa de Pedro.
Volume da Esfera
A esfera surge da revolução de uma semicircunferência. Observe:
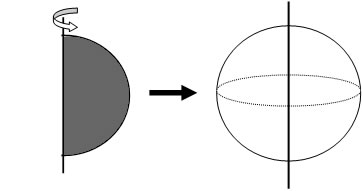
Esse corpo circular possui inúmeras aplicações cotidianas. Seu volume depende do tamanho do raio, que é à distância do centro da esfera a qualquer ponto da extremidade. A fórmula matemática utilizada para determinar o volume da esfera é a seguinte:
Exemplo 1
Uma esfera possui raio medindo 5 cm. Determine o volume dessa esfera.
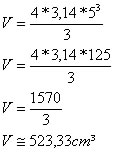
A esfera possui 523,33 cm³ de volume.
Exemplo 2
Duas esferas metálicas de raios r e 2r são fundidas e moldadas em forma de um cilindro de altura 3r. Qual é o raio R do cilindro?
Volume da esfera metálica de raio r
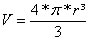
Volume da esfera metálica de raio 2r
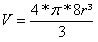
Somar os volumes das esferas
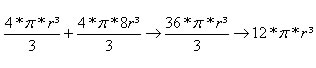
Volume do cilindro será igual ao volume das esferas.
Volume do cilindro = π * r² * h, onde altura igual a 3r. Vamos determinar o raio R do cilindro.
π * R² * 3r = 12 * π * r³
R² = 12 * r³ / 3r
R² = 4r²
R = 2r
Temos que o raio do cilindro é 2r.
Exemplo 3
Vamos considerar que o raio do planeta Terra meça, aproximadamente, 6380 km. Determine o volume do planeta.
Exemplo 4
Uma fábrica de bombons deseja produzir 20 000 unidades no formato de uma esfera de raio 1 cm. Determine o volume de cada bombom e a quantidade de chocolate necessária para produzir esse número de bombons.
Volume de cada bombom
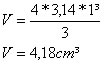
A quantidade de chocolate necessária para a produção das 20 000 unidades é de:
4,18 * 20 000 = 83 600 cm³
Sabemos que 1cm³ = 1 ml, então 83 600 cm³ corresponde a 83 600 ml de chocolate ou 83,6 quilos.
A fábrica irá gastar 83,6 quilos de chocolate, e o volume de cada bombom será de 4,18 cm³.
Volume da Pirâmide
O volume da pirâmide corresponde a um terço do volume de um prisma de mesma altura e base. Portanto, a expressão matemática utilizada no cálculo do volume da pirâmide é:
V = Ab * h
Ab = área da base
h = altura
É importante ressaltar que uma pirâmide pode possuir inúmeras bases. Ela pode ter a base triangular, quadrangular, pentagonal, hexagonal, heptagonal, entre outras. Dessa, o cálculo da área da base está ligado ao polígono correspondente. Nas pirâmides triangulares e quadrangulares, as fórmulas para o cálculo da área da base são as seguintes:
Triângulo
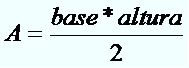
Quadrangular
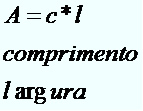
Nas bases onde os polígonos possuem mais de quatro lados, a área é calculada através da expressão:
Ab = p * a
p = semiperímetro (metade do produto entre o número de lados e o comprimento do lado)
a = apótema (distância entre o centro da base e ponto médio de um lado)
Exemplo 1
Uma pirâmide de base quadrangular possui altura medindo 2 metros e cada lado da base com medida igual a 3 metros. Determine o volume dessa pirâmide.
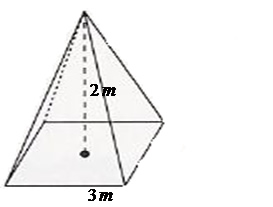
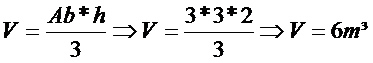
Exemplo 2
Uma indústria irá fabricar uma peça no formato de uma pirâmide de base triangular com as medidas indicadas na figura. Sabendo que serão fabricadas 500 peças maciças de aço, determine o volume total de aço que será gasto na produção dessas peças.
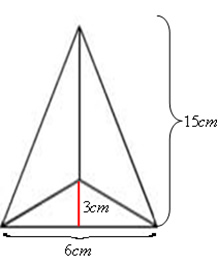
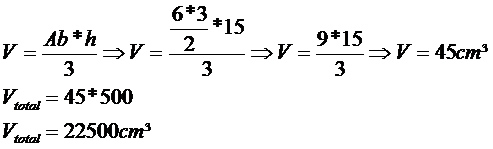
Exemplo 3
A figura representa uma pirâmide de base pentagonal com lados regulares medindo 12 metros e a apótema da base medindo 8,2 metros, aproximadamente. Sabendo que a altura dessa pirâmide é igual a 20 metros, qual será sua capacidade sabendo que 1 m³ corresponde a 1000 litros?
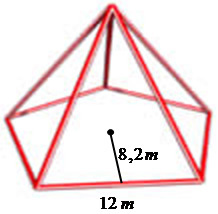
Área da base e Volume
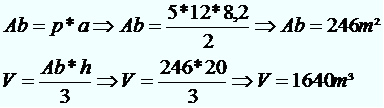
Se 1m³ corresponde a 1000 litros, temos que:
1640m³ = 1640 * 1000 = 1 640 000 litros de capacidade.
Volume de um Sólido Geométrico
Podemos ter muitas definições para a palavra volume, mas para a Matemática é o espaço ocupado por um corpo. Todo sólido geométrico possui volume e ocupa espaço.
A unidade usual de volume é metros cúbicos (m³).
Em determinadas situações o volume pode ser grande, nesse caso iremos representá-lo usando a seguinte unidade:
1m³ (metro cúbico) = 1000 litros
Em situações em que o volume é muito pequeno podemos usar:
1cm³ = 1 ml (mililitro)
Em situações cotidianas usamos:
1 litro = 1000cm³ (centímetro cúbico) = 1dm³ (decímetro cúbico)
Podemos concluir que as principais unidades usuais de m³ (metros cúbicos) são:
1m³ = 1000 litros
1cm³ = 1 ml (mililitro)
1 litro = 1000cm³ (centímetro cúbico) = 1dm³ (decímetro cúbico)
Exemplos de sólidos geométricos:
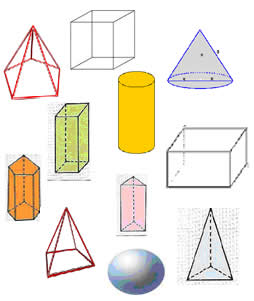
Fórmulas para Cálculo de Volumes
produto da área da base pela medida da altura. De uma forma geral, podemos aplicar a seguinte fórmula:
V = Ab x h
Ab = área da base
h = altura
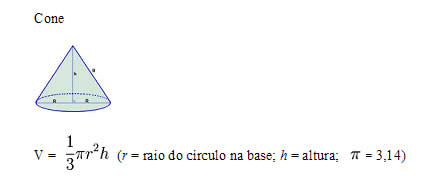
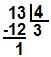
Volume do Cilindro
O cilindro é uma figura espacial formada através da revolução de uma região quadrada ou retangular. Observe:
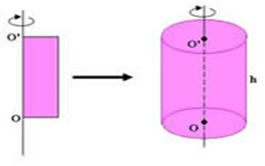
Como todo sólido geométrico o cilindro possui volume. O volume de um cilindro é dado através da multiplicação da área da base pela altura. O cilindro possui está presente em diversas situações cotidianas pela sua capacidade de armazenamento de substâncias, por exemplo, botijão de gás, reservatório de água ou combustível entre outros. As duas bases de um cilindro possuem a forma circular e a área do círculo é determinada pela expressão π * r². Assim temos que o volume do cilindro é dado pela seguinte expressão matemática:
V = π * r² * h
Exemplo 1
Uma empresa irá fabricar latinhas de alumínio para uma indústria de refrigerantes. A lata precisa comportar a quantidade de 450 ml de refrigerante. Considerando que o formato da lata é semelhante a um cilindro e que a altura seja de 10 cm, qual será a medida do raio da base?
Temos que 450 ml corresponde a 450 cm , pois 1 cm³ = 1 ml
V = π * r² * h
450 = 3,14 * r² * 10
450 = 31,4 * r²
450/31,4 = r²
r² = 14,3
r = 3,8 cm (aproximadamente)
O raio da base devera medir aproximadamente 3,8 cm
Exemplo 2
Uma indústria irá produzir dois tipos de copos com formato cilíndrico. O copo azul terá as seguintes medidas 5 cm de raio da base e 12 cm de altura e o copo verde 3 cm de raio da base e 18 cm de altura. Qual dos copos possuirá o maior volume?
Copo azul
V = π * r² * h
V = 3,14 * 5² * 12
V = 3,14 * 25 * 12
V = 942 cm³
Copo verde
V = π * r² * h
V = 3,14 * 3² * 14
V = 3,14 * 9 * 18
V = 508,68 cm³
O copo azul possuirá o maior volume.
Exemplo 3
Uma lata de óleo de soja possui as seguintes dimensões: raio da base medindo 4,5 cm e altura igual a 16 cm. Considerando que o conteúdo da lata seja de 900 ml, calcule a parte não ocupada da lata de óleo.
Vamos determinar o volume total da lata
V = π * r² * h
V = 3,14 * 4,5² * 16
V = 3,14 * 20,25 * 16
V = 1017,36 cm³
Obtendo o volume da parte não ocupada
1 017,36 – 900 = 117,36 ml
A parte não ocupada da lata corresponde a 117,36 ml.
Volume do Cone
O cone é formado através da revolução de um triângulo retângulo sobre um eixo. Observe:
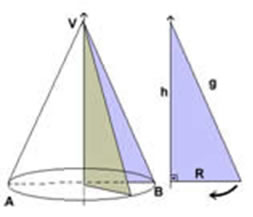
A base de um cone é uma região de formato circular com o raio de medida r. A distância do vértice ao centro da base formando um ângulo de 90º recebe o nome de altura (h) do cone. O comprimento da face lateral é denominado geratriz (g) do cone.
Para calcularmos o volume do cone multiplicamos a área da base pela medida da altura e dividimos o resultado por três. Observe:
Exemplo 1
Um copo será fabricado no formato de um cone com as seguintes medidas: 4 cm de raio e 12 cm de altura. Qual será a capacidade do copo?
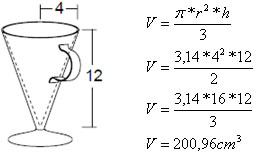
Exemplo 2
Uma fábrica de doces e balas irá produzir chocolates na forma de guarda-chuva, com as seguintes medidas: 8 cm de altura e 3 cm de raio de acordo com a ilustração. Qual a quantidade de chocolate utilizada na produção de 2000 peças?
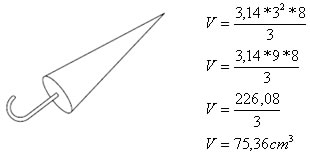
Cada chocolate possui 75,36 cm³ de volume. A fábrica quer produzir 2000 peças, então:
2000 * 75,36 = 150 720 cm³
Lembrando que 1 cm³ = 1 ml, temos 150 720 ml de chocolate que corresponde a 150,72 litros.
Exemplo 3
Uma casquinha de sorvete possui o formato de um cone reto com altura de 10 cm e raio da base medindo 5 cm. Determine o volume da casquinha.
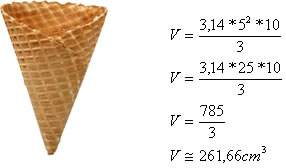
O volume da casquinha é de 261,66 cm³, que corresponde a, aproximadamente, 261 ml.
Exemplo 4
Um reservatório possui volume de aproximadamente 3000 m³ e diâmetro da base medindo 24 metros. Determine a altura deste reservatório.
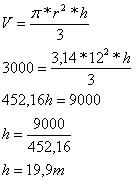
A altura do reservatório é de aproximadamente 20 metros.
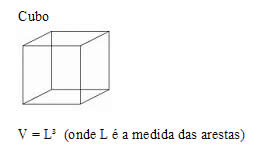
Volume do Cubo
O cubo é denominado hexaedro regular e é um dos cinco sólidos de Platão. Por ser considerado um sólido, possui volume.
Dizemos que volume é a quantidade de espaço ocupado por um corpo ou a capacidade de armazenamento que um corpo possui. O volume de um cubo depende da medida de sua aresta, consideramos apenas uma medida, pois o cubo possui todas as arestas de tamanhos iguais e seu volume é apresentado pela expressão V = a³, onde a corresponde à medida da aresta.
O volume de um cubo é determinado através do produto da área da base pela altura, como já foi dito que as arestas do cubo possuem medidas iguais, então temos que V = Ab * a ou V = a * a * a → V = a³. Observe:
As unidades mais usadas para expressar capacidade são as seguintes: m³ (metro cúbico), cm³ (centímetro cúbico), dm³ (decímetro cúbico). Onde respeitam as seguintes relações:
1 m³ = 1000 litros
1 dm³ = 1 litro
1 cm³ = 1 mililitro ou 1 ml
De acordo com as seguintes relações, concluímos que:
Um cubo formado por arestas medindo 1 metro (m) cada, possui capacidade de 1000 litros, pois: V = 1m * 1m * 1m = 1m³.
Um cubo formado por arestas medindo 1 decímetro (dm) cada, possui capacidade de 1 litro, pois: V = 1dm * 1dm * 1dm = 1dm³ = 1 litro.
Um cubo formado por arestas medindo 1 centímetro (cm) cada, possui capacidade de 1 ml, pois: V = 1cm * 1cm * 1cm = 1cm³ = 1 ml.
Exemplo
Dado um cubo de 10 cm de aresta, determine quantas bolinhas de diâmetro igual a 1cm ele comporta.
Resolução:
De acordo com o que foi demonstrado, temos que o volume total do cubo corresponde a:
V = 10cm * 10cm * 10cm = 1000 cm³. Como a bolinha possui diâmetro medindo 1cm, podemos formar as arestas do cubo com 10 bolinhas enfileiradas. Observe:
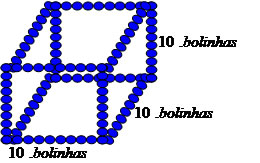
Portanto, o cubo com 10 cm de aresta comporta 1000 bolinhas com 1 cm de diâmetro.
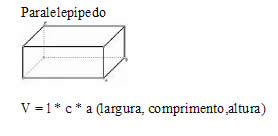
Volume do Paralelepípedo
armazenar substâncias. O volume de um paralelepípedo é calculado através da multiplicação entre a área da base e a altura, ou para ser mais prático: comprimento x largura x altura, considerando sempre que as unidades de comprimento das dimensões sejam as mesmas. Vários objetos possuem o formato de um paralelepípedo, por exemplo, uma caixa, uma piscina, um aquário entre outros.
1 m³ (metro cúbico) = 1000 L (litros)
1 dm³ (decímetro cúbico) = 1 L
1 cm³ (centímetro cúbico) = 1 mL (mililitro)
Exemplo 1
Um aquário possui o formato de um paralelepípedo com as seguintes dimensões:
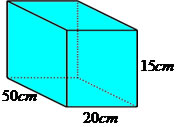
Determine quantos litros de água são necessários para encher o aquário.
V = comprimento x largura x altura
V = 50 cm x 20 cm x 15 cm
V = 15000 cm³ (centímetros cúbicos)
Como foi informado que 1 cm³ corresponde a 1 ml, temos que 15000 cm³ é igual a 15000 ml ou 15 litros.
Exemplo 2
Uma prova internacional de natação é disputada em uma piscina olímpica com as seguintes dimensões: 50 metros de comprimento, 25 metros de largura e 3 metros de profundidade. Determine o volume e quantos litros de água são necessários para encher essa piscina.
V = comprimento x largura x profundidade
V = 50 metros x 25 metros x 3 metros
V = 50 x 25 x 3
V = 3750 m³ (metros cúbicos)
Temos que 1 m³ corresponde a 1000 litros, portanto 3750 * 1000 = 3 750 000 litros (três milhões setecentos e cinquenta mil litros).
Exemplo 3
O degrau de uma escada lembra a forma de um paralelepípedo com as seguintes dimensões: 1 m de comprimento, 0,5 m de largura e 0,4 m de altura. Determine o volume total de concreto gasto na construção dessa escada sabendo que ela é constituída de 20 degraus.
Volume do degrau
V = 1 m x 0,5 m x 0,4 m
V = 0,20 m³
Volume total da escada
0,20 x 20
4 m³ ou 4 mil litros de concreto.
Volume do Tronco da Pirâmide
A intersecção de um plano a uma determinada altura da base de uma pirâmide gera uma nova figura geométrica espacial denominada tronco da pirâmide.
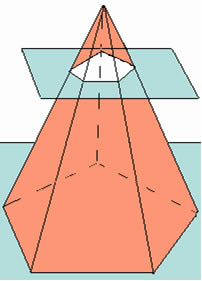
O tronco da pirâmide é composto de duas bases com áreas de medidas diferentes, lembrando que a área depende do formato da figura plana em questão. No tronco existem duas alturas que não devem se confundidas: uma delas é a altura (h) do tronco, que é a distância entre as duas bases de modo que o ângulo formado entre uma reta imaginária e as bases seja igual a 90º. A outra medida corresponde à geratriz (g) do tronco, que se refere à altura da lateral da face, a qual forma com as bases ângulos diferentes de 90º.
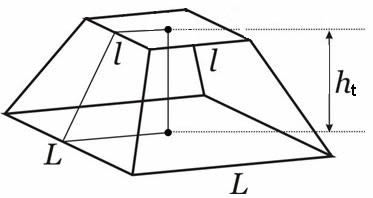
A expressão utilizada na determinação do volume de um tronco da pirâmide em relação à medida da altura e das áreas das bases é:
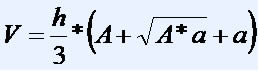, em que:
V = volume
h = altura do tronco da pirâmide
A = área da base de maior superfície
a = área da base de menor superfície
Exemplo 1
Um tronco da pirâmide possui como bases dois quadrados de lados medindo 16 e 24 centímetros, respectivamente. Sabendo que a altura do tronco é equivalente a 42 cm, determine seu volume.
Área quadrado maior: 24 * 24 = 576 cm²
Área quadrado menor: 16 * 16 = 256 cm²
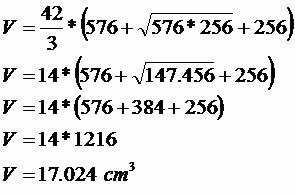
Exemplo 2
Um reservatório possui as dimensões de um tronco da pirâmide com lado da base menor medindo 2 m e lado da base maior medindo 8 m. Considerando que a medida da altura corresponde a √8 m, calcule sua capacidade de armazenamento.
Área quadrado maior: 8 * 8 = 64 m²
Área quadrado menor: 2 * 2 = 4 m²
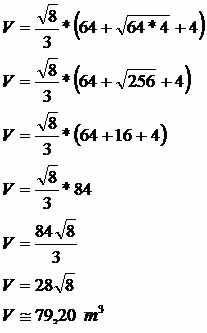
Sabemos que 1 m³ (metro cúbico) corresponde a 1000 litros, dessa forma 79,20 m³ correspondem a 79,20 * 1000 que é equivalente a 79.200 litros. Portanto, o reservatório armazena em sua capacidade máxima 79.200 litros.
Volume do tronco de cone
O tronco de cone de bases paralelas é obtido realizando-se uma secção transversal num cone circular.
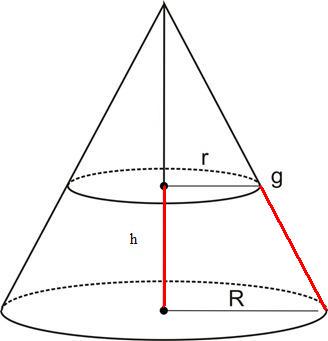
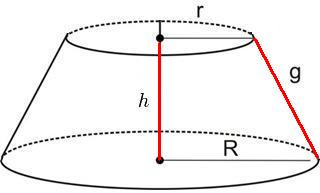
Elementos do tronco de cone:
Base do tronco (B) → é a maior base do tronco
Altura (h) → distância entre as duas bases
Raio da base (R) → é o raio da maior base
Geratriz (g)
O volume do tronco de cone de bases paralelas é dado fazendo a diferença entre os volumes dos dois cones obtidos após a secção transversal. Colocando o volume em função dos raios das bases e da altura do cone, obtemos a fórmula:
Onde
h → é a altura do tronco de cone.
R → é o raio da base maior.
r → é o raio da base menor.
Exemplo. Calcule o volume de um tronco de cone de bases paralelas de altura 10 cm, raio da base maior medindo 8 cm e raio da base menor com 4 cm de comprimento.
Solução: temos que
h = 10 cm
R = 8 cm
r = 4 cm
V = ?
Substituindo os valores na fórmula do volume, obtemos:
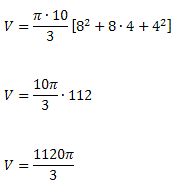
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática