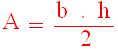As civilizações antigas já utilizavam a geometria no seu cotidiano. Antes de Cristo, a Mesopotâmia, o Egito utilizava de seus conhecimentos geométricos para a construção de obras, para controlar as enchentes, para remarcar os limites das propriedades agrícolas, construção de pirâmides e outras.

Logo após, surgiu na Grécia vários filósofos (estudiosos), como Tales, Platão, Perseu, Eudoxo, Euclides de Alexandria, Pitágoras, que demonstraram e provaram algumas teorias na geometria, dentre elas podemos destacar: Semelhança de triângulo, Teorema de Pitágoras, Criação da trigonometria.

A geometria que estudamos no ensino fundamental e médio é dividida em Geometria plana, Geometria no espaço (geometria espacial) e Geometria analítica.

Ângulos no círculo

A relação entre ângulos e círculo é muito importante no estudo da geometria. Diversos assuntos ligados à astronomia possuem relações estreitas com ângulos no círculo ou na circunferência. Podemos ter ângulos com vértice no centro, no interior ou no exterior de um círculo, cada um apresentando características e propriedades diferentes. Vejamos cada um desses casos:

1. Ângulo com vértice no centro da circunferência – Ângulo central.

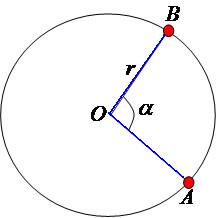
Propriedade: o ângulo central apresenta a mesma medida do arco formado por seus lados, ou seja: 

2. Ângulo cujo vértice é um ponto da circunferência – Ângulo Inscrito.

Propriedade: a medida do ângulo inscrito equivale à metade da medida do arco formado por seus lados, ou seja:

Exemplo: Determine o valor de α sabendo que o arco AB mede 60^o.

Solução:


3. Ângulo com vértice exterior à circunferência – Ângulo excêntrico externo.

Propriedade: o ângulo α equivale à metade da diferença entre as medidas dos arcos formados pelos seus lados, ou seja:

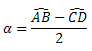
Exemplo: Determine o valor de α na figura abaixo.

 
4. Ângulo com vértice no interior da circunferência – Ângulo excêntrico interno.

Propriedade: o ângulo excêntrico interno possui medida igual à metade da soma dos arcos formados pelos seus lados, ou seja:

Exemplo: Determine o valor de α na figura abaixo.

Solução:

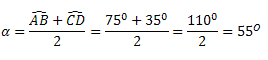
Aplicações do Cálculo da Área de uma Circunferência

Existem muitos objetos e construções que lembram a forma de uma circunferência ou que possuem contorno na forma de uma circunferência, como as rodas de uma bicicleta ou de um automóvel, anéis, placas de trânsito, tampas de panelas, contornos de praças circulares, volante de um automóvel entre outros.

Calculamos a área de uma região limitada por uma circunferência aplicando a seguinte fórmula:


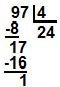
Onde:

∏ (pi) = aproximadamente 3,14
r = raio da circunferência

Exemplo 1

Qual a área de uma praça que tem raio medindo 12 metros?
A = ∏r²

A = 3,14 * 12²
A = 3,14 * 144
A = 452,16 m²

A área da praça é de 452,16 m²

Exemplo 2

Se a área de uma região circular é de 379,94 m², qual o valor do seu raio?
A = ∏r²

379,94 = 3,14 * r²
r² = 379,94 / 3,14
r² = 121 (aplicar raiz quadrada)
r = 11 m
O raio da praça mede 11 metros.

Aplicações do Teorema de Tales

O Teorema de Tales possui diversas aplicações no cotidiano, constituindo uma importante ferramenta da Geometria no cálculo de distâncias inacessíveis e nas relações envolvendo semelhança entre triângulos. A melhor forma de visualizar as aplicabilidades do Teorema proposto por Tales de Mileto é através de alguns exemplos.

Exemplo 1

Calcule o comprimento da ponte que deverá ser construída sobre o rio, de acordo com o esquema a seguir.

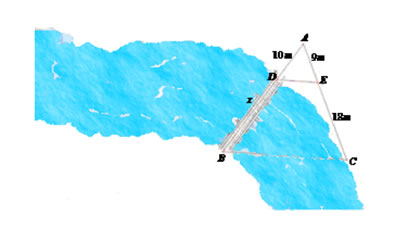
De acordo com a figura temos um triângulo ABC e o segmento DE dividindo o triângulo, sendo formado o triângulo ADE. As informações que temos são as medidas dos seguintes segmentos: AD = 10m, AE = 9m, EC = 18m e DB = x. O valor de DB será determinado através do Teorema de Tales que diz: “retas paralelas cortadas por transversais formam segmentos proporcionais.” Desse modo, podemos estabelecer a seguinte relação:

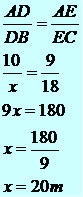
Portanto, a ponte terá 20 metros de comprimento.

Exemplo 2

Determine o valor de x na figura.

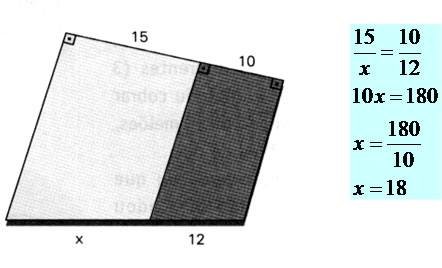
Exemplo 3

Na figura, as retas r, s e t são paralelas, de acordo com Teorema de Tales determine p valor de x.

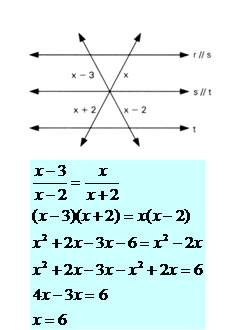
Axiomas e Postulados

estudo da geometria se baseia em dois princípios:

• Conceitos sobre: ponto, reta e plano.
• As propostas evidentes chamadas de axiomas ou postulados.

Postulado 1
Existem infinitos pontos no universo.

Postulado 2
Existem infinitas retas no universo.

Postulado 3
Existem infinitos planos no universo.

Postulado 4
Existem infinitos pontos em cada reta e fora dela.


Postulado5
Por um ponto passam infinitas retas.


Postulado 6
Existem infinitos pontos dentro e fora do plano.


Postulado 7
Para determinar uma reta é necessário dois pontos distintos.


Postulado 8
Para determinar um plano é necessário 3 pontos.
Aqui podemos utilizar o exemplo de uma cadeira tripé.

Pois a extremidade dos três pés se apóia sempre em um só plano.

Postulado 9
Se dois pontos distintos pertencem a um plano a reta que passa por esses pontos pertence ao plano.

A α
B α
A r
B r
Portanto r α

Postulado 10
Todo ponto de uma reta forma com ela duas semi-retas.


Postulado 11
Uma reta que tem um só ponto comum com o plano ela fura o plano.
Uma reta que tem dois pontos comuns ao plano ela está contida no plano.

r fura o plano α em C então C α
B α
A α
Então a reta t α

Cálculo Aproximado de Áreas

A Geometria é um ramo da Matemática responsável pelas diversas formas geométricas encontradas na natureza e construídas pelo homem. Consiste em uma ciência de maior aplicabilidade no cotidiano, ao comprar uma corda estamos usando a Geometria, pois se trata de uma medida linear. Se precisarmos azulejar o piso de uma casa devemos informar ao depósito de material de construção a área em metros quadrados (m²) do piso a ser azulejado. Alguns objetos recebem o nome de sólidos, em razão da sua propriedade de armazenamento, por exemplo: uma garrafa, um copo, reservatórios de água e etc., possuindo as seguintes unidades usuais de medida: o litro (l), o mililitro (ml) entre outras.

Vamos fixar o nosso estudo no cálculo de áreas irregulares.

A Geometria estabelece uma fórmula matemática para o cálculo de cada área, dependendo do formato da figura.
Já nos casos onde o formato é irregular podemos usar algumas técnicas para se obter um resultado satisfatório. Observe a região irregular a seguir, ela representa a planta de um terreno, onde cada 1cm² representa 1km² no real.

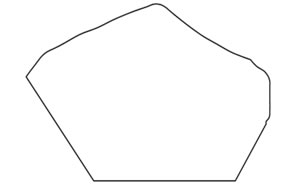
Vamos quadricular a figura e considerar cada quadradinho como 1cm² de área.

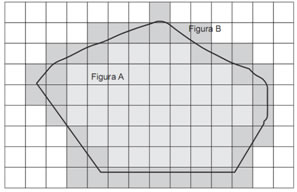
Solução
Ao contarmos os quadradinhos da região A (interna) temos: 43cm²
Os quadradinhos da região B (cobrindo a figura) somam: 80cm²
A área da figura está entre 43cm² e 80cm².

Para calcularmos aproximadamente a área da figura devemos obter a média aritmética das regiões A e B:

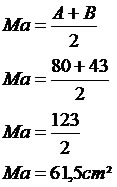
Como cada 1cm² corresponde a 1km², temos que a área do lote é de 61,5 km².

Cilindro

produtos gasosos e líquidos, máquinas industriais, embalagens de produtos para consumo e etc. Vamos conhecer as propriedades, os elementos e as classificações de um cilindro.
O cilindro é um sólido geométrico gerado pela rotação de uma superfície retangular.
Observe:

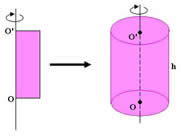
                               cilindro de revolução

Elementos de um cilindro

O cilindro é composto por duas bases, com a forma circular de raio (r), altura (h) e geratriz (medida da lateral do cilindro). No cilindro circular reto, a geratriz forma com a base um ângulo de 90º e possui a mesma medida da altura (h). No cilindro oblíquo, as medidas da altura (h) e da geratriz são diferentes.

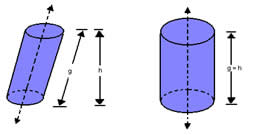
Cilindro oblíquo                     Cilindro circular reto


Planificação do cilindro



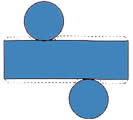
Áreas correspondentes ao cilindro

Área da base do cilindro

Por ser uma circunferência, calculamos a área da base de um cilindro aplicando a expressão: Ab = пr² (п = 3,14).


Área lateral do cilindro

Veja que a lateral do cilindro, quando planificado, forma um retângulo cujas dimensões são: altura h e base 2 пr (Observe que a base do retângulo é o comprimento da circunferência que forma a base do cilindro)


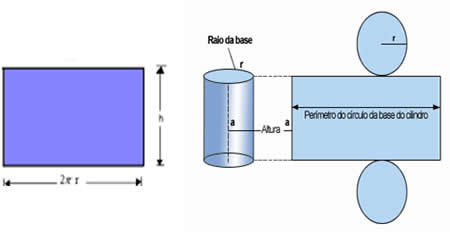
A expressão que permite calcular a área lateral do cilindro é: A_L = 2 * п *r * h, onde п = 3,14, r: raio e h: altura.


Área total

A área total de um cilindro é dada somando a área lateral e as duas áreas das bases.
A expressão matemática que permite realizar esse cálculo utilizando a altura (h), o raio da base (r) e o valor de п (3,14) é:

A_T = 2пr(h +r)


Volume do cilindro

Dado um cilindro de raio (r) e altura (h), calculamos seu volume através do produto da área da base pela altura. Observe a expressão:

V = п r²h

Classificação de Triângulos

O triângulo é considerado uma importante figura no ramo da Geometria, pois através dele podemos estabelecer várias relações fundamentais, como exemplo temos uma relação muito importante utilizada na Geometria e na Trigonometria, que é o Teorema de Pitágoras.
Podemos definir o triângulo como um polígono formado por três segmentos de retas que se cruzam duas a duas, formando três vértices, três ângulos e três lados.
Os triângulos se classificam quanto ao tamanho da medida dos seus lados e quanto à medida de seus ângulos.

Classificação de um triângulo quanto à medida de seus lados.

Triângulo equilátero: possui os três lados com medidas iguais.
Triângulo isósceles: possui dois lados com medidas iguais.
Triângulo escaleno: possui os três lados com medidas diferentes.



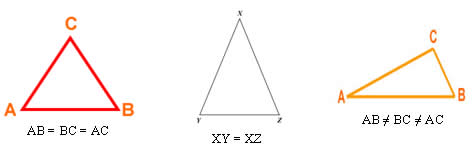
Classificação de um triângulo quanto à medida de seus ângulos

Triângulo acutângulo: possui todos os ângulos com medidas menores que 90º.
Triângulo retângulo: possui um ângulo com medida igual a 90º.
Triângulo obtusângulo: possui um ângulo obtuso, maior que 90º.


       acutângulo                                               retângulo                                                         obtusângulo

Comprimento da circunferência

cálculo do seu perímetro é dado pelo comprimento da circunferência (contorno do círculo), pois um círculo é contornado por uma circunferência que é formada pela união das extremidades de uma linha aberta .

O cálculo do comprimento da circunferência (perímetro) foi obtido da seguinte forma: Como todas as circunferências são semelhantes entre si, ou seja, todas pertencem ao mesmo centro foi concluído que a razão entre os comprimentos de qualquer circunferência pelo seu respectivo diâmetro será sempre uma mesma constante.

E essa constate foi provada pelo matemático grego Arquimedes de Siracura que seria aproximadamente 3,14, e como esse valor não era exato foi estipulado que poderia ser representado pela letra do alfabeto grego π, facilitando os cálculos. Assim, convencionou que π ≈ 3,14.

Com essas informações podemos concluir uma maneira prática de encontrar o valor do perímetro de um círculo ou cumprimento de uma circunferência.

Iremos estipular: c como sendo o comprimento, r sendo o raio da circunferência.

 c = constante
2r

 c = π
 2r

c = 2 π r

Quando medimos os lados de uma região, estamos determinando o valor do seu perímetro. No caso das regiões circulares não podemos adotar tal metodologia, pois não podemos definir a medida dos lados desse tipo de região. Para determinar a medida do comprimento de uma região circular, utilizamos a medida de seu raio, mas somente isso não é suficiente.

Devido à relação comprimento/diâmetro nas regiões circulares, conseguimos descobrir um valor constante, aproximadamente igual a 3,14. Esse número irracional ficou conhecido por “pi”, o qual é representado pelo símbolo π. Em qualquer região circular basta dividirmos o comprimento da mesma, pela medida do diâmetro, que encontraremos o valor correspondente a 3,14 aproximadamente.

Com base nessa descoberta, o comprimento de uma região limitada por uma circunferência é calculada através da expressão matemática C = 2 * π * r. Por exemplo, se uma região circular possui raio medindo 8 metros, seu comprimento será calculado da seguinte maneira:

C = 2 * 3,14 * 8
C = 50,24 m

A descoberta desse número constante, relacionado às regiões circulares, é atribuída ao matemático grego Arquimedes. Na fórmula, temos que:

C: comprimento da região circular
π: aproximadamente igual a 3,14
r: medida do raio da região circular

Conceitos básicos de circunferência

O estudo da circunferência na trigonometria é de grande importância, pois ela proporciona a construção de um ciclo trigonométrico que facilita o trabalhado no estudo trigonométrico de ângulos que não são agudos, tornando o estudo da trigonometria mais completo.

O que é circunferência?

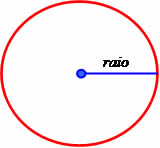
Imagine um ponto P qualquer, todos os pontos distintos e eqüidistantes a ele irá formar uma circunferência.



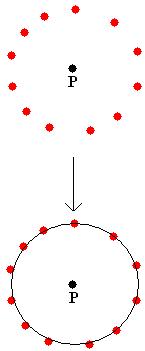
Esse ponto P é considerado o centro da circunferência, pois todos os pontos que pertencem à circunferência estão na mesma distância do ponto P. Essa distância é chamada de raio da circunferência.

Arco de circunferência

Arco de uma circunferência é, de uma maneira mais formal, uma parte do comprimento de uma circunferência que é delimitado por dois pontos quaisquer que pertence à circunferência. Veja como é feita essa representação:

Considere uma circunferência de centro P e com A e B pontos pertencentes a essa circunferência:



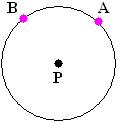
As partes delimitadas da circunferência pelos pontos A e B são chamadas de arcos da circunferência. Esses arcos possuem medidas de comprimentos.
Dois pontos quaisquer pertencentes a uma circunferência formam dois arcos.



O arco de medida x é representado por  e .

O arco de medida y é representado por .

Sabemos que um arco de circunferência é delimitado por dois pontos que pertencem à circunferência, se esses pontos forem iguais, ou seja, estiverem localizados no mesmo lugar na circunferência, o arco será nulo ou de uma volta completa.



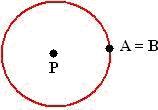
Ângulo central

Todo ângulo é formado pela abertura de dois segmentos de reta. O ângulo central é formado por duas retas que partem do centro e vão de encontro com os dois pontos da circunferência. A abertura dessas duas retas determina a medida do ângulo.



O arco subtende o ângulo central , formado pelos segmentos de reta AP e PB,
ou seja:

med ( ) = med ( ).

Condição de existência de um triângulo

Sabemos que um triângulo é formado por três lados que possuem uma determinada medida, mas essas não podem ser escolhidas aleatoriamente como os lados de um quadrado ou de um retângulo, é preciso seguir uma regra.

Só irá existir um triângulo se, somente se, os seus lados obedeceram à seguinte regra: um de seus lados deve ser maior que o valor absoluto (módulo) da diferença dos outros dois lados e menor que a soma dos outros dois lados. Veja o resumo da regra abaixo:

| b - c | < a < b + c
| a - c | < b < a + c
| a - b | < c < a + b

Exemplo:
Com os três segmentos de reta medindo 5cm, 10cm e 9cm, podemos formar um triângulo?
Vamos aplicar a regra da condição de existência de um triângulo para todos os lados.
|10 – 9| < 5 < 10 + 9
1 < 5 <19 (VERDADEIRO)

|9 – 5| < 10 < 9 + 5
4 < 10 < 14 (VERDADEIRO)

|5 – 10| < 9 < 10 + 5
5 < 9 < 15 (VERDADEIRO)

Quando um lado não obedece à regra não é possível existir um triângulo.

Cone

Ao olharmos ao nosso redor, nos deparamos com figuras geométricas de formas variadas, estudos são desenvolvidos no intuito de desvendar as propriedades de tais situações geométricas. Uma forma conhecida e muito utilizada é o cone, figura que iremos estudar.
O cone reto é uma figura de base circular gerada pela revolução de um triângulo retângulo.



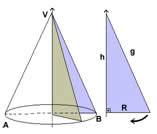
Elementos de um cone

O cone é composto por uma base circular de raio (r), altura (h), vértice e lateral chamada de geratriz. No cone reto a altura é perpendicular ao centro da base de raio (r), isto é, a altura e o centro da base formam um ângulo de 90º.

Classificação e exemplos

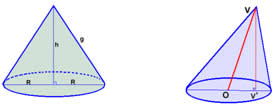
  Cone Reto                                            Cone Oblíquo

Planificação do cone


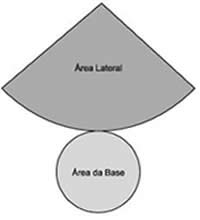
Áreas pertencentes ao cone

Área da base

A área da base de um cone é a região limitada por um círculo, que pode ser calculada pela expressão: A_b = пr² (п = 3,14).

Área lateral

A área lateral de um cone é formada pela geratriz do cone, podemos considerá-la como o raio, veja que a planificação lateral do cone é um arco de circunferência de comprimento 2пr, pois este arco é o comprimento da base do cone. Podemos calcular a área lateral do cone utilizando a seguinte fórmula: A_L = пrg.

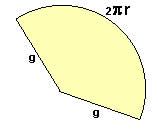
Área total

Calculamos a área total de um cone adicionando a área lateral e a área da base, para isso podemos utilizar a seguinte expressão:

A_t = пr (g+r)

Volume

O volume do cone é calculado multiplicando a área da base pela altura.

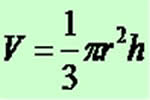
Conhecendo os Elementos de um Polígono

Polígono é a região limitada por segmentos de reta, os quais constituem linhas fechadas. Observe:

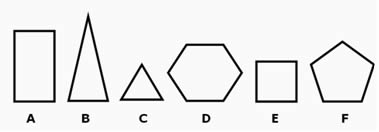
Alguns polígonos são nomeados de acordo com o número de lados e outros de acordo com algumas características essenciais. Veja:

A: retângulo (polígono com quatro lados, em que os paralelos possuem a mesma medida)

B: triângulo isósceles (polígono de três lados, em que dois possuem a mesma medida)

C: triângulo equilátero (os três lados possuem a mesma medida)

D: hexágono (polígono com seis lados)

E: quadrado (possui os quatro lados com medidas iguais)

F: pentágono (polígono com cinco lados)

Em um polígono podemos identificar os seguintes elementos: vértices, lados, ângulos internos, ângulos externos, diagonais. O triângulo é o único dos polígonos que não possui diagonal.

Os vértices constituem o ponto de encontro de dois segmentos laterais.

Os lados são as linhas poligonais que se encontram dois a dois em cada vértice.

Os ângulos internos e externos são formados pelo encontro de dois lados consecutivos.

As diagonais são segmentos de reta que unem dois vértices não consecutivos. Lembre-se, que o triângulo não possui diagonal.

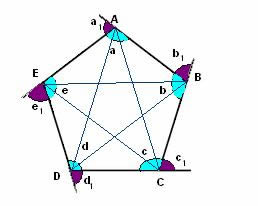
No polígono acima temos:

Lados: AB, BC, CD, DE, AE

Vértices: A, B, C, D e E

Ângulos internos: a, b, c, d, e

Ângulos externos: a1, b1, c1, d1, e1

Diagonais: AD ou DA, AC ou CA, BE ou EB, BD ou DB, CE ou EC

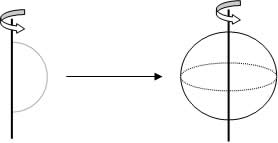
Corpo Esférico

Podemos definir a esfera como um sólido geométrico que possui corpo curvilíneo, cujos pontos estão eqüidistantes do centro, ou seja, possuem a mesma distância do centro interno. A esfera é um sólido gerado pela revolução completa de um semicírculo em um eixo. Observe ilustração:




Podemos encontrar a estrutura esférica em diversas situações, veja os exemplos:

     Núcleo do átomo                      Molécula da água

             Sol                                               Lua 

Área de uma esfera e Volume de uma esfera

Exemplo 1
Calcule o volume de uma esfera com raio medindo 10 cm. Considere п = 3,14.


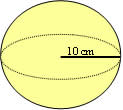
V = (4пr³)/3
V = (4*3,14*10³) / 3
V = (12,56 * 1000) /3
V = 12560 / 3
V = 4186,66 cm³


Exemplo 2
Qual a área de um corpo esférico com diâmetro medindo 18 cm. Considere п = 3,14.

A = 4пr²
A = 4 * 3,14 * 9²
A = 1017,36 cm²


Exemplo 3
Calcule o volume e a área de um corpo esférico que possui raio medindo cerca de 5 metros. Considere п = 3,14.

V = (4пr³)/3
V = (4*3,14*5³) / 3
V = (12,56 * 125) /3
V = 1570 / 3
V = 523,33 cm³

A = 4пr²
A = 4 * 3,14 * 5²
A = 12,56*25
A = 314 cm²

Duas Retas Paralelas Cortadas por uma Transversal

Ao construirmos o esquema envolvendo duas retas paralelas, cortadas por uma transversal, definiremos os valores dos ângulos utilizando a semelhança de triângulos. Observe a representação:

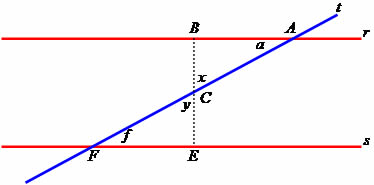
As retas r e s paralelas são cortadas pela transversal t. A determinação da relação entre os ângulos da intersecção se dá mediante o estabelecimento de um segmento auxiliar representado por BE. Note que, com o auxílio do segmento, conseguimos determinar os triângulos ABC e CEF, os quais possuirão ângulos semelhantes.

Os ângulos a e f são denominados alternos internos e os ângulos x e y são opostos pelo vértice. Dessa forma, temos que a = f e x = y e que os triângulos ABC e CEF são semelhantes, portanto ABC ~ CEF. Os ângulos com vértice nos pontos B e E possuem 90º devido ao segmento BE ser perpendicular as retas r e s.

Se uma reta transversal corta duas retas paralelas, teremos a formação de ângulos alternos internos e ângulos opostos pelo vértice.

Fórmula de Heron

Heron de Alexandria é o responsável por elaborar uma fórmula matemática que calcula a área de um triângulo em função das medidas dos seus três lados. A fórmula de Heron de Alexandria é muito útil nos casos em que não sabemos a altura do triângulo, mas temos a medida dos lados.
Em um triângulo de lados medindo a, b e c podemos calcular a sua área utilizando a fórmula de Heron:

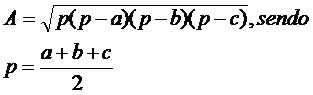
Exemplo 1
Calcule a área do triângulo a seguir:

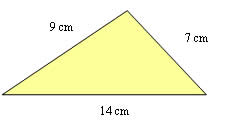
p = (9 + 7 + 14) / 2
p = 30 / 2
p = 15

A = √15(15 – 9)(15 – 7)(15 – 14)
A = √15 * 6 * 8 * 1
A = √720
A = 26,83 cm²(aproximadamente)

Exemplo 2
Utilizando a Fórmula de Heron, calcule a área da região com as seguintes medidas:

26cm, 26cm e 20cm

p = (26 + 26 + 20) / 2
p = 72 / 2
p = 36

A = √36(36 – 26)(36 – 26)(36 – 20)
A = √36 * 10 * 10 * 16
A = √57600
A = 240 cm²

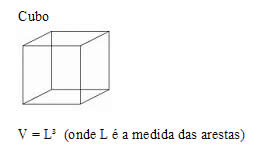
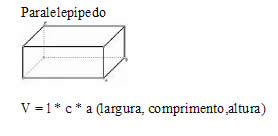
Fórmulas para Cálculo de Volumes

produto da área da base pela medida da altura. De uma forma geral, podemos aplicar a seguinte fórmula:

V = Ab x h

Ab = área da base
h = altura

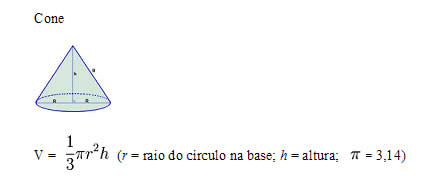
O Teorema de Pitágoras no Cotidiano

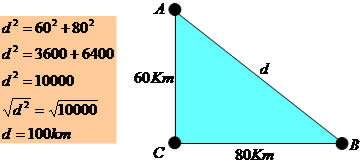
O Teorema de Pitágoras possui inúmeras aplicações nas diversas áreas de atuação do homem. A área de transportes é considerada muito importante para o desenvolvimento de um país, o teorema de Pitágoras está presente nela contribuindo na sua logística e no desenvolvimento cotidiano, no intuito de dinamizar cada vez mais o setor.

Imagine a seguinte situação:

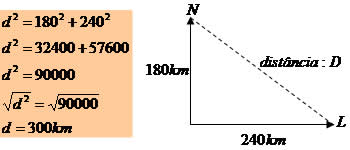
Dois navios A e B partem em sentidos diferentes: o primeiro para o norte e o segundo para o leste, o navio A com velocidade constante de 30 Km/h e o navio B com velocidade constante de 40 Km/h. Qual será a distância entre eles após 6 horas?

Distância percorrida pelo navio A após 6 horas:
D = 30*6 = 180 Km

Distância percorrida pelo navio B após 6 horas:
D = 40 * 6 = 240 Km

Veja o esquema:

Aplicando o Teorema de Pitágoras


Exemplo 2

De posse de um mapa (veja figura), o motorista de um caminhão de entrega de eletrodomésticos precisa saber qual a distância entre as cidades A e B, pois dependendo da distância precisa abastecer o caminhão para não ter surpresas desagradáveis na viagem, falta de combustível ou atraso na entrega.

Polígonos Inscritos e Circunscritos

Na geometria costumamos relacionar algumas figuras, entre elas a circunferência e os polígonos. As duas propriedades seguintes pertencem a essa relação:

 Qualquer polígono regular é inscritível em uma circunferência.
 Qualquer polígono regular e circunscritível a uma circunferência.

Temos que polígonos regulares são figuras em que todos os seus lados e todos os seus ângulos são congruentes, isto é, possuem medidas iguais. Observe alguns polígonos inscritos e circunscritos a seguir:

Polígonos regulares inscritos

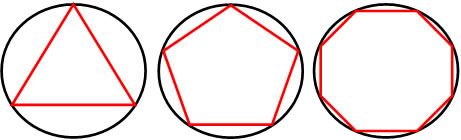
No caso dos polígonos inscritos apresentados, observe que o vértice de cada polígono é tangente à circunferência. Esse ponto de tangência divide a circunferência em partes iguais, as quais recebem o nome de arco de circunferência. O triângulo inscrito divide a circunferência em 3 arcos de comprimentos iguais, o pentágono em 5 arcos iguais e o octógono em 8 arcos iguais. Cada segmento de reta que forma o lado do polígono é considerado uma corda da circunferência.


Polígonos regulares circunscritos

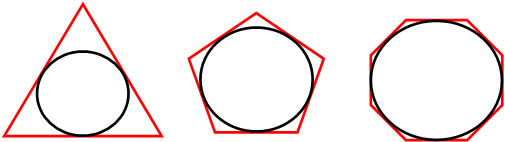
Princípios da geometria

importantes e essenciais para o aprendizado de Geometria Plana ou Geometria de espacial.

►Ponto

Na matemática ponto não tem uma definição, mas é representado por letras maiúsculas: A, B, C,D, ... , Z), Veja alguns exemplos:


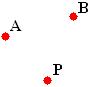
A, B e P representam pontos.

►Reta

Para formarmos uma reta precisamos de no mínimo dois pontos. A reta é representada por letras minúsculas (a, b, .... , r, s, t, .....,z), e em suas extremidades temos setas, pois a reta é infinita para os dois sentidos.



• Para fazermos a relação de ponto e reta usamos a relação de pertinência:

A  t (A pertence a t)

Encontramos retas em algumas coisas do nosso cotidiano: como o encontro de duas paredes, lado de uma mesa, cabo de vassoura, são aproximações grosseiras de retas, mas que nos ajuda a visualizar melhor.




Além de usarmos as letras minúsculas na representação das retas, podemos utilizar os seus pontos na sua representação:



Temos no exemplo acima uma reta a letra que a representa é t. Pertencem a reta t os pontos A e G, então podemos fazer uma outra representação para a reta t:


 -------- sempre em cima dos pontos deve ser colocado uma reta com duas setas
pois a reta pode ser prolongada nos dois sentidos.


►Plano

Para diferenciarmos a representação do plano com a representação da reta, a sua representação ficou com letras minúsculas, mas do alfabeto grego: α (alfa), β (beta), ...
Como a reta o plano também é infinito.



Em um plano β estão contidas retas e tem pontos que pertencem a esse mesmo plano:
• Para fazermos uma relação entre ponto e reta utilizamos a relação de pertinência:
A  r  ;  B s  ;  C t  ;  D v  ;  E r

• Para fazermos uma relação entre ponto e plano utilizaremos a relação de pertinência:
A β  ;  B β  ;  C β  ;  D β  ;  E β


• Para fazer a relação entre reta e plano, utilizamos a relação de inclusão:
v β ; r β ; t β  ; s β

Relação entre Volumes

O volume de um corpo é a característica que ele possui em armazenar algo. Todos os corpos tridimensionais possuem essa característica, como exemplo citaremos: o cubo, o paralelepípedo, o prisma, o cone, a esfera, a pirâmide, o cilindro entre outros. Uma importante relação entre volumes é que dois corpos com estruturas diferentes podem possuir o mesmo volume, isto é, a mesma capacidade. Observe:

Exemplo 1

Em uma padaria há dois tipos de forma de bolo, formas 1 e 2, como mostra a ilustração a seguir.

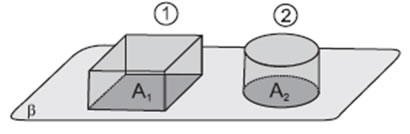
Sejam L o lado da base da forma quadrada, r o raio da base da forma redonda, A1 e A2 as áreas das bases das formas 1 e 2, V1 e V2 os seus volumes, respectivamente. Se as formas têm a mesma altura h, para que elas comportem a mesma quantidade de massa de bolo, qual é a relação entre a medida do raio r do lado L?
Resolução:

Devemos realizar a igualdade entre os volumes dos dois sólidos. Podemos considerar que a figura sobre a base quadrada seja um cubo. Dessa forma:

Volume do cubo = L³
Volume do cilindro = π * r * h

Igualdade entre os volumes
Volume do cubo = volume do cilindro
L³ = π * r² * h
Como as alturas são iguais temos que L = h

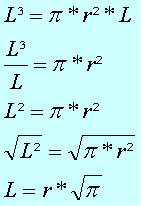
Portanto, a relação entre o lado L e o raio r é L = r * √π.

Exemplo 2

A altura de um cilindro é igual ao dobro da altura de outro cilindro. Para que eles possuam o mesmo volume, qual deve ser a relação entre os raios da base?

V1 = π * r² * h
V2 = π * r² * 2h

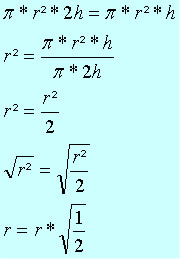
Soma dos Ângulos Internos de um Polígono Regular

Polígonos são regiões limitadas por segmentos de reta. O encontro dos segmentos de reta formam os vértices e os ângulos da figura. O polígono mais simples é o triângulo, que possui três lados, três vértices e três ângulos.

Veja a tabela com os dados de alguns polígonos regulares.

A soma dos ângulos internos de um polígono é dada pela expressão:

S = (n – 2 )*180º, onde n = número de lados.

Para calcular o valor de cada ângulo é preciso dividir a soma dos ângulos internos pelo número de lados do polígono.


Exemplo 1
Qual é a soma dos ângulos internos de um heptágono regular?

O heptágono possui 7 lados.
S = (n – 2) * 180º
S = (7 – 2) * 180º
S = 5 * 180º
S = 900º
A soma dos ângulos internos de um heptágono é 900º.

Exemplo 2
Qual a soma dos ângulos internos de um icoságono (20 lados)?

Aplicando a fórmula:
S = (n – 2) * 180º
S = (20 – 2) * 180º
S = 18 * 180º
S = 3240º
A soma dos ângulos internos de um icoságono é 3240º.

Podemos utilizar a fórmula da soma dos ângulos internos para calcular o número de lados de qualquer polígono, desde que a soma dos ângulos internos seja dada.

Exemplo 3
Quantos lados possui um polígono cuja soma dos ângulos internos é igual a 2340º?

S = (n – 2) * 180º
2340º = (n – 2) * 180º
2340º = 180n – 360º
2340 + 360 = 180n
2700 = 180n
180n = 2700
n = 2700/180
n = 15

O polígono possui 15 lados.

A soma dos ângulos externos de qualquer polígono regular é 360º.
Para calcular a medida do ângulo externo de um polígono é preciso dividir 360º pelo número de lados da figura poligonal.

Exemplo 4
Quanto mede o ângulo externo do hexágono?

O hexágono possui seis lados, então:

ai = 360º / 6
ai = 60º

Cada ângulo externo de um hexágono mede 60º.

Teorema da Bissetriz Interna

Os triângulos são formas geométricas que sempre despertaram a curiosidade de matemáticos de várias épocas. A investigação desse polígono levou à descoberta de várias propriedades e teoremas, dentre eles, talvez o mais famoso, o teorema de Pitágoras. Diante da observação dos elementos de um triângulo, outros teoremas foram elaborados, ampliando as características e descobertas desta figura tão fascinante.

Veremos mais um teorema e sua vasta aplicação na geometria e na trigonometria, o teorema da bissetriz interna.

O teorema da bissetriz interna diz que: uma bissetriz interna de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes.

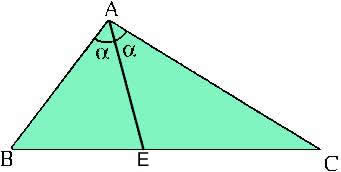
Ou seja:

Vejamos alguns exemplos de aplicação desse teorema.

Exemplo 1. Determine o valor de x no triângulo abaixo sabendo que AP é bissetriz do ângulo A.

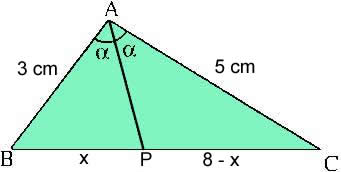
Solução: Utilizando o teorema da bissetriz interna, temos que:

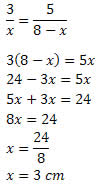
Portanto, x = 3 cm.

Exemplo 2. Calcule a medida do lado AC do triângulo abaixo, sabendo que AG é bissetriz do ângulo A.

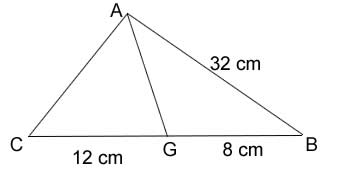
Solução: Pelo teorema da bissetriz interna, temos que:

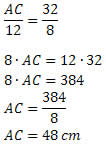
Portanto, o lado AC do triângulo possui 48 cm de comprimento.

Observe que o teorema da bissetriz interna apresenta semelhanças com o teorema de Tales.